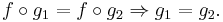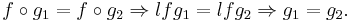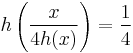Monomorphism

This page is about the mathematical term. For other uses, see Monomorphic (disambiguation) or Polymorphism (disambiguation).

In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation 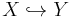X \hookrightarrow Y.

In the more general setting of category theory, a monomorphism (also called a monic morphism or a mono) is a left-cancellative morphism, that is, an arrow f : X → Y such that, for all morphisms g1, g2 : Z → X,

f \circ g_1 = f \circ g_2 \Rightarrow g_1 = g_2.

Monomorphisms are a categorical generalization of injective functions; in some categories the notions coincide, but monomorphisms are more general, as in the examples below.

The categorical dual of a monomorphism is an epimorphism, i.e. a monomorphism in a category C is an epimorphism in the dual category Cop. Every section is a monomorphism, and every retraction is an epimorphism.

Contents

Terminology

The companion terms monomorphism and epimorphism were originally introduced by Nicolas Bourbaki; Bourbaki uses monomorphism as shorthand for an injective function. Early category theorists believed that the correct generalization of injectivity to the context of categories was the cancellation property given above. While this is not exactly true for monic maps, it is very close, so this has caused little trouble, unlike the case of epimorphisms. Saunders Mac Lane attempted to make a distinction between what he called monomorphisms, which were maps in a concrete category whose underlying maps of sets were injective, and monic maps, which are monomorphisms in the categorical sense of the word. This distinction never came into general use.

Another name for monomorphism is extension, although this has other uses too.

Relation to invertibility

Left invertible maps are necessarily monic: if l is a left inverse for f (meaning 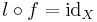l \circ f = \operatorname{id}_{X}), then f is monic, as

f \circ g_1 = f \circ g_2 \Rightarrow lfg_1 = lfg_2 \Rightarrow g_1 = g_2.

A left invertible map is called a split mono.

A map f : X → Y is monic if and only if the induced map f∗ : Hom(Z, X) → Hom(Z, Y), defined by 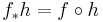f_{*}h = f \circ h for all morphisms h : Z → X , is injective for all Z.

Examples

Every morphism in a concrete category whose underlying function is injective is a monomorphism. In the category of sets, the converse also holds so the monomorphisms are exactly the injective morphisms. The converse also holds in most naturally occurring categories of algebras because of the existence of a free object on one generator. In particular, it is true in the categories of groups and rings, and in any abelian category.

It is not true in general, however, that all monomorphisms must be injective in other categories. For example, in the category Div of divisible abelian groups and group homomorphisms between them there are monomorphisms that are not injective: consider the quotient map q : Q → Q/Z. This is clearly not an injective map; nevertheless, it is a monomorphism in this category. To see this, note that if q ∘ f = q ∘ g for some morphisms f,g : G → Q where G is some divisible abelian group then q ∘ h = 0 where h = f − g (this makes sense as this is an additive category). This implies that h(x) is an integer if x ∈ G. If h(x) is not 0 then, for instance,

h\left(\frac{x}{4h(x)}\right) = \frac{1}{4}

so that

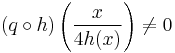(q \circ h)\left(\frac{x}{4h(x)}\right) \neq 0,

contradicting q ∘ h = 0, so h(x) = 0 and q is therefore a monomorphism.

Properties

Related concepts

There are also useful concepts of regular monomorphism, strong monomorphism, and extremal monomorphism. A regular monomorphism equalizes some parallel pair of morphisms. An extremal monomorphism is a monomorphism that cannot be nontrivially factored through an epimorphism: Precisely, if m=g ∘ e with e an epimorphism, then e is an isomorphism. A strong monomorphism satisfies a certain lifting property with respect to commutative squares involving an epimorphism.

See also

References